3차원 공간에서 다수의 물체를 그릴 때 그리는 순서를 고려하지 않고 그리면 다음과 같이 어떤 오브젝트가 더 앞에 있는지 알 수 없다.
이를 해결하기 위해선, 우리가 깊이 값을 파악하고 앞에 있는 물체를 뒤에 있는 물체가 덮어쓰지 않게 하기 위해 픽셀 별로 깊이 값을 계산해야 한다.
깊이 값
이를 해결하기 위해서는 픽셀별로 앞에 있는지, 뒤에 있는지 순서를 파악하기 위한 정보가 필요하다.
화면으로 쓸 NDC는 2차원이였으므로 z를 통한 판별이 불가능하다, 대신 NDC 공간을 3차원으로 확장해보자
이러한 깊이를 지정할 때 필요한 것이 절두체 (Frustum) 인데
투영 공간과 카메라의 화각 등을 생각해보면 무한대에서 무한대로 진행되는 공간이라고 할 수 있다.
하지만 우리가 이런 무한대의 공간의 깊이 값을 산출하기 보다는 NDC처럼 '그릴 범위'를 지정해서 사용하겠다는 뜻
'무한대' 로 이루어진 투영 공간의 일부분만을 자른 입체 도형을 '절두체' 라고 한다.
절두체를 구하면 다음 사진과 같이 사각뿔 모양의 도형이 생기는데,
카메라와 가까운 면을 near plane, 그릴 수 있는 최대 범위를 far plane 이라고 한다.
near plane은 대부분 0, far plane 은 1을 주게 된다.
근평면과 원평면을 기반으로 NDC 공간을 3차원으로 확장하면 다음과 같다.
OpenGL 은 깊이 범위에 [-1, 1] 을 사용하고 , DirectX 는 깊이 범위에 [0, 1]을 사용한다.
깊이 값을 나타낼땐, 대부분 이미지를 사용하는게 대부분인데 이미지 라는것은 [0, 1] 의 색상만 사용하기 때문에 -1을 사용하지 않고 0으로 시작하는 것들이 있다.
최종 투영 행렬
기존 행렬에서 쓸모없던 한 열을 사용해 깊이 값까지 구할 수 있는 최종 행렬을 완성해보자
P⋅vview=[vxvyvz1][da0i00dj000k100l0]=[da⋅vxd⋅vy?vz]
깊이 값은 x, y에 직교한다. 따라서 i, j의 값은 0이다.
P⋅vview=[vxvyvz1][da0000d0000k100l0]=[da⋅vxd⋅vy?vz]
근평면과 원평면에 대응되는 NDC 좌표는 다음과 같다.
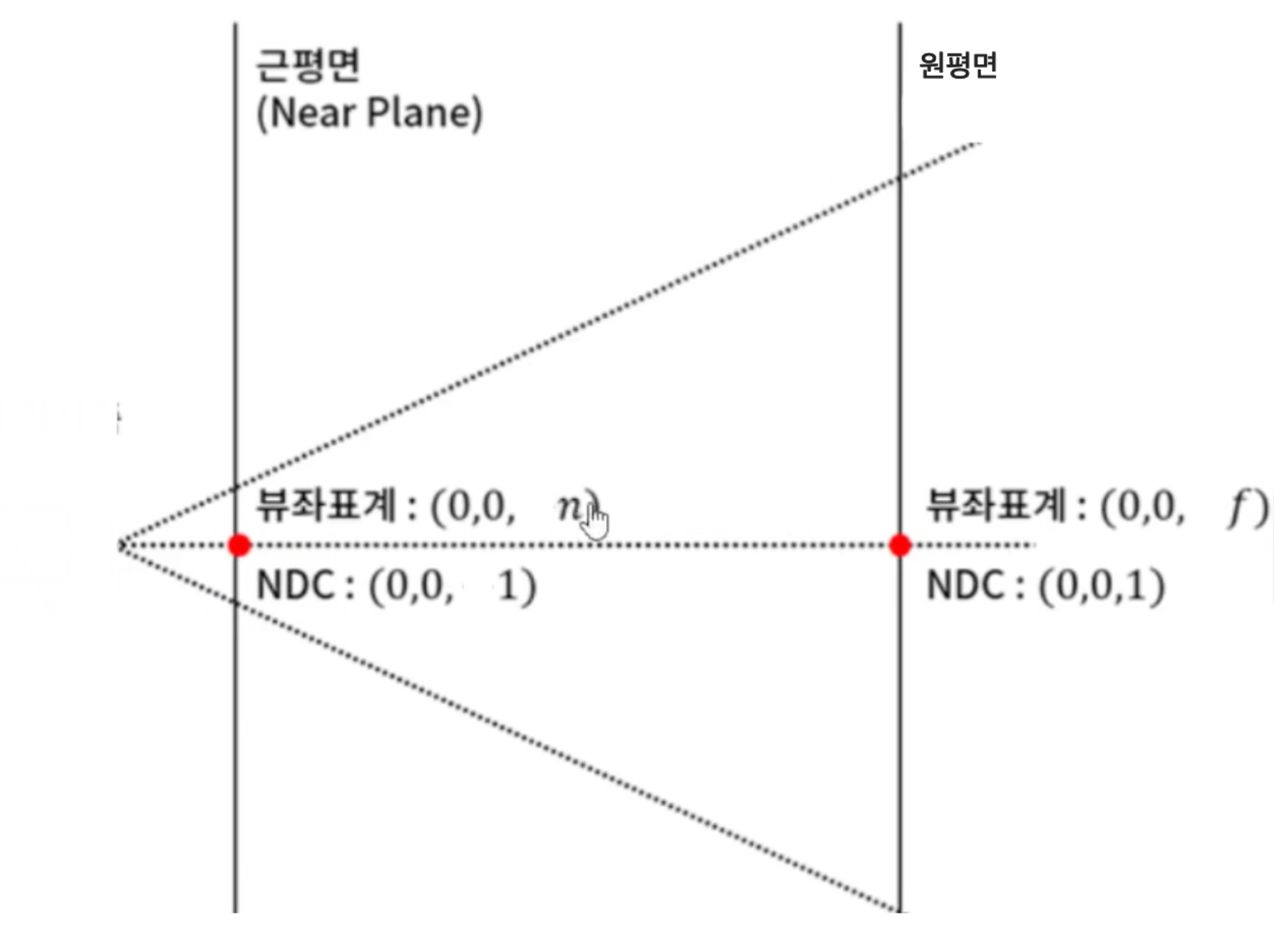
그렇다면 각각의 클립좌표는 다음과 같을 것이다.
P⋅vview=[00n1][da0000d0000k100l0]=[00?n.]
P⋅vview=[00f1][da0000d0000k100l0]=[00?f]
여기서 우리는 ?의 값을 구해야 하는데, 동차좌표예서 마지막 값 으로 나눈다는것을 생각해보자
첫 행렬에서 ?의 값을 n으로 나눴을때는 0이 나와야 하며
두 번째 행렬에서 ?의 값을 f로 나눴을때는 1이 나와야 한다.
그렇다면 첫 행렬의 ?는 0이여야 하고
두 번째 ? 는 f여야 한다.
(0,0,0,n)(0,0,f,f)
이를 통해 연립방정식을 구하게 되면
kn+l=0kf+l=f
이고 l 을 소거시켜 k를 구한다
kn−kf=−fk(n−f)=−fk=ff−n
이 k값을 연립방정식에 대입하여 l 값을 구한다.
ff−n⋅f+l=fl=−fnf−n
이를 적용하면 최종 행렬이 얻어진다.
P=[da0000d0000ff−n100−fnf−n0]
