무게중심좌표
이전 세 점의 아핀결합에서 사용된 세 스칼라 (s, t, 1 - s - t)는 모두 실수이므로, 이들을 묶어서 하나의 3차원 벡터를 생성할 수 있다. 이렇게 아핀 결합의 스칼라를 묶어 만든 좌표를 무게중심좌표 ( Barycentric Coordinate ) 라고한다.
무게중심좌표는 삼각형에 관련된 정보를 담고 있기에, 삼각형에 관련된 기능을 구현할 때 유용하게 활용된다

.세 점의 아핀 결합이 삼각형이 되려면 모든 스칼라의 값이 [0, 1] 범위 내에 있어야 했다.
무게중심좌표를 구성하는 스칼라 값이 하나라도 [0, 1] 범위를 벗어난다면 아핀 결합으로 생성된 점은 삼각형 외부에 있다고 판단할 수 있다. 이러한 성질을 활용하면 주어진 점이 삼각형 영역의 내부에 있는지 외부에 있는지 판단할 수 있는데 이를 위한 수식을 유도해보자
아핀 결합식은 다음과 같았다.
$$ P' s = s \cdot P_{1} + t \cdot P_{2} + (1 - s - t) \cdot P_{3} $$
여기서 (1 - s - t) * P3을 분배한 후 s, t 로 점들을 묶어보자 다음과 같이 나타난다.
$$P' = s \cdot P_{1} + t \cdot P_{2} + P_{3} -s P_{3}-tP_{3}$$
여기서 s와 t로 묶고, 남은 P3를 좌측으로 넘겨보자
$$ (P'- P_{3}) = s(P_{1} - P_{3}) + t(P_{2} - P_{3}) $$
다음과 같은 수식이 나타난다.
이 전의 글에서 살펴본 바와 같이 점에서 점을 빼면 벡터가 되므로
P' - P3는 P3에서 새로운 점 P'로 가는 벡터
P1 - P3는 P3에서 P1으로 가는 벡터
P2 - P3는 P3에서 P@로 가는 벡터이다.
이 세 벡터를 각각 u, v, w로 표시하면 위 식은 다음과 같이 정리된다.
$$\vec{w} = s\cdot\vec{u} + t\cdot\vec{v}$$
이 세 벡터가 서로 선형 독립의 관계라면, 벡터 w는 3차원 벡터 공간 안에 존재하는 모든 벡터를 생성할 수 있다,
따라서, 세 점의 아핀 결합은 평면의 모든 점을 만들어 낸다.
여기서 아핀 결합으로 생성되는 점 P'가 삼각형 내부에 있는지 판별하기 위해 내적을 활용해보자.
벡터 w에 u와 v를 내적하면 다음과 같은 수식이 나온다.
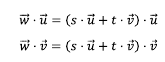
내적 연산한 수식을 분배법칙에 따라 풀어주면 다음과 같이 전개된다.

여기서 s를 소거하기 위해 위의 식에는 (u dot v)를, 아래의 식에는 (u dot u)를 곱해 전개해보자.
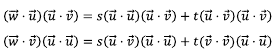
윗 식에서 아래 식을 빼 s를 소거하고 t만 남긴다. 식을 풀어 t에 대해 정리를 하면 다음과 같은 식이 만들어진다.

다시 예전 식으로 돌아가서 s에 대해 정리하기 위해 양변에 (v dot v)와 (u dot v)를 곱해보자
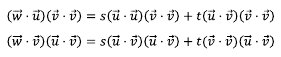
윗 식에서 아래 식을 빼 t를 소거하고 s에 대해 정리한 식은 다음과 같다.
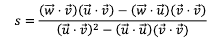
이렇게 얻어진 무게중심좌표 세 값 모두 [0, 1] 범위 안에 있다면 점 P'는 삼각형 안에 있고, 세 값중 하나라도 [0. 1] 범위를 벗어나면 P'는 삼각형 밖에 있다고 판단할 수 있다.
이 식을 사용할 때 주의할 점은 분모의 결과가 0이 나올수도 있기 때문인데, 두 벡터가 평행해져 선형 종속의 관계를 이룰 수 있기 때문이다.

이러한 삼각형을 퇴화삼각형( Degenerate Triangle ) 이라고 한다.
픽셀화
무게 중심 좌표를 이용하면, 삼각형을 포함하는 각 픽셀을 찾고 해당 픽셀이 도형의 내부 혹은 외부에 있는지를 판단할 수 있다.
각각의 s, t, 1 - s - t 의 값이 다 [0, 1] 사이에 있는지만 판단하면 된다.
'Graphics > 이론' 카테고리의 다른 글
| 삼각함수 (1) | 2023.07.20 |
|---|---|
| 아핀 결합 ( Affine Combination ) (1) | 2022.12.21 |
| 원근 투영 변환 - 깊이값( Perspective projection transformation - Depth ) (1) | 2022.11.17 |
| 원근 투영 변환 ( Perspective projection transformation ) (4) | 2022.11.14 |
| 뷰 변환 ( View Transformation, Camera Transformation ) (0) | 2022.11.08 |
