
직각 삼각형은 밑변, 빗변, 높이 세 가지 요소로 이루어져 있다.
이러한 직각 삼각형의 세 개의 변에서 두 개의 변을 골라 비의 값을 정한다고 하면
빗변/높이, 빗변/밑변 등 여러개의 비를 구할 수 있다.
이 중 주로 사용하는 세 가지의 삼각비는 다음과 같다.

이 삼각비를 함수의 개념으로 확장해서 해당 비의 각을 정의역으로 두고
비의 값을 취했을 때 이 값은 항상 [-1, 1] 사이에 대응된다.

정의역의 원소 x 와 공역의 원소 y 에 대한 대응 관계를 y = sin(x) 같은 함수로 나타낼 수 있게 된다.
데카르트 평면의 좌표계에서 만들어지는 평면의 모든 각(360도)을 일반화 시킨 것을
삼각함수라고 한다.
삼각함수를 사용할 때는 직각삼각형에 국한되어서 사용하기 보다는, 평면을 모두 포함하는 단위원을 기반으로 삼각함수를 분석하게 된다.

빗변이 항상 1인 원을 뜻한다.
이 상태에서 삼각함수를 사용하게 되면은 다음과 같은 그래프가 만들어지게 된다.
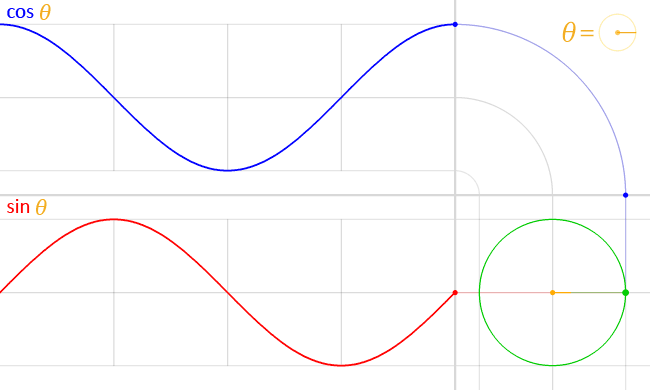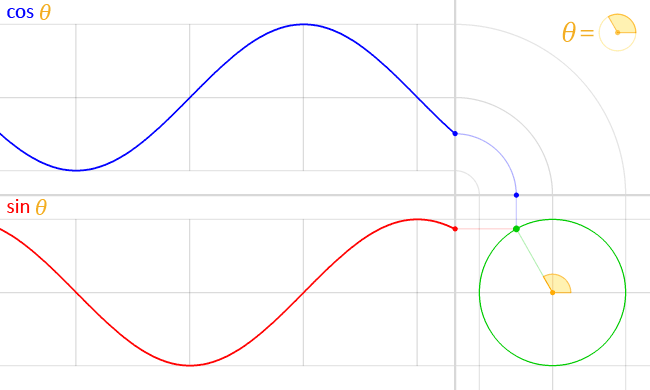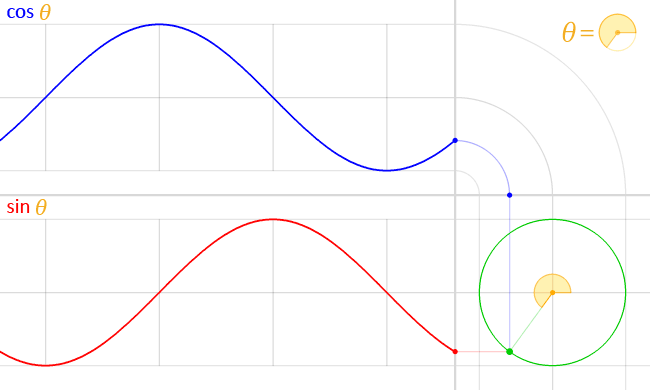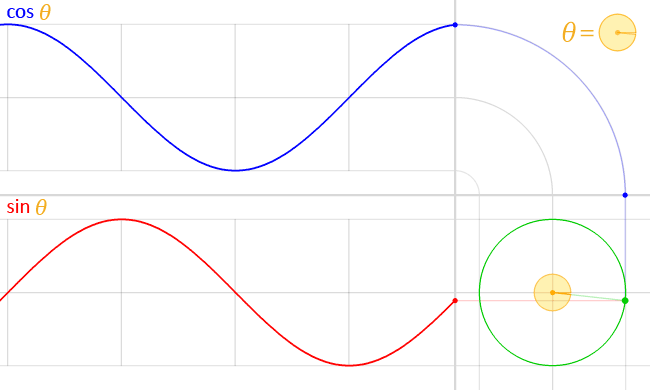
이 것이 sin 함수와 cos 함수의 그래프이다.
삼각비의 각에 따른 값이 어떻게 변환되는지를 볼 수 있다.
사인 함수와 코사인 함수는 항상 [-1, 1] 범위를 일정하게 반복되는 패턴을 가진다.
사인과 코사인 함수는 한 바퀴(360도)를 기준으로 반복된다.
축을 기준으로 좌우를 포갰을 때 코사인 함수는 데칼코마니처럼 좌우 대칭인 반면, 사인 함수는 상하가 반전된 형태를 가진다.

tan 함수는 90도와 270도에서 값이 존재하지 않는다.
cos = 밑변 / 빗변
sin = 높이 / 빗변 인데
단위원에서 빗변은 항상 1이므로
cos = 밑변
sin = 높이
가 되고, 빗변은 항상 cos 과 sin의 영향을 받는다고 할 수 있다.
tan = 높이 / 밑변 이므로
tan = sin / cos 라고 할 수 있다.
cos 은 90도와 270 도에서 0 값을 가지고 있는데, 분모가 0이면 계산이 되지 않으므로 tan는 90도와 270도에서 값이 존재하지 않는다.
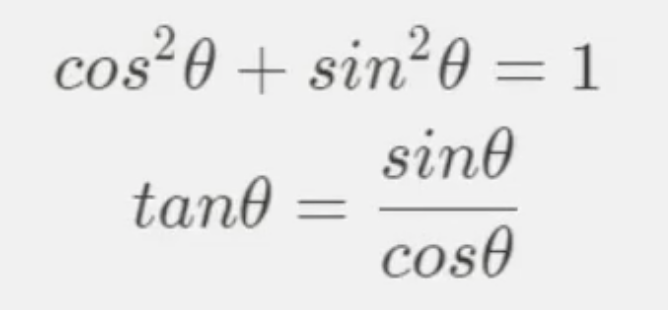
피타고라스의 정리를 생각해보자
빗변은 항상 1로 고정되어 있으니 밑변 * 밑변 + 높이 * 높이 = 1 이라는 값이 나온다.
즉 cos 에 제곱을 한 값과 sin 에 제곱을 한 값을 더한 값은 항상 1이다.
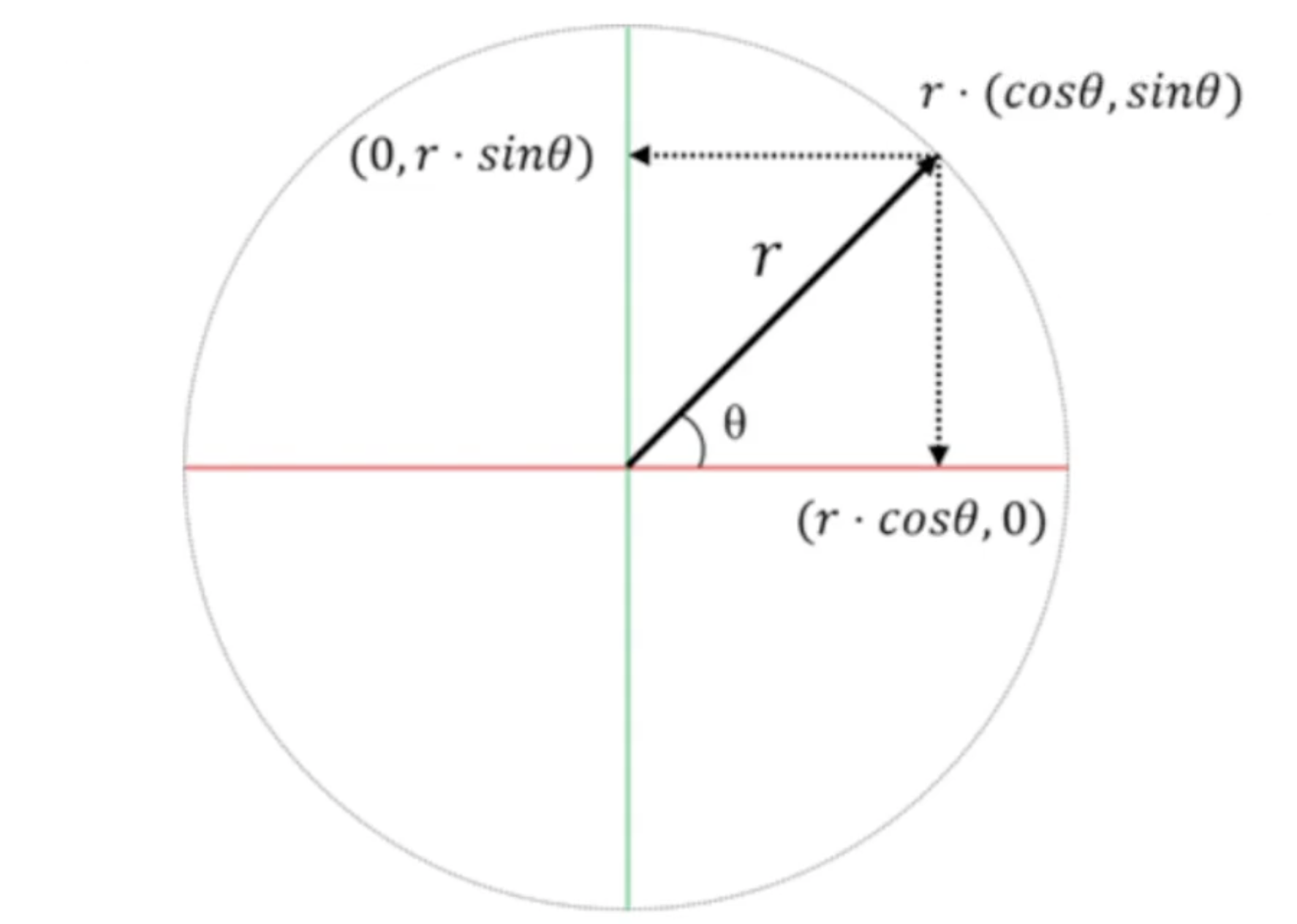
임의의 원의 반지름 값을 r 이라고 했을 때, r (원호) 의 좌표는 (cos, sin) 벡터에 r 배 한 결과이다.
삼각비를 이루기 때문에 위의 공식은 항상 유효하다.


실벡터공간의 표준 기저 벡터 (1, 0) 과 (0, 1)도 결국 크기가 1인 벡터이다.
크키가 1인 벡터인 것은 일반화 시킨다고 했을 때, 평면의 모든 크기가 1인 벡터들은 (cos, sin) 로 일반화 시킬 수 있다.
이 중 두 종류가 e1 과 e2 이고 이 값은 0도와 90도일때를 의미한다.
각도법(Degree)
원을 360개로 균일하게 나누고, '도' 라고 사용해 각을 표현
약수가 많이 나오는 ( 2로 나누든, 4로 나누든, 8로 나누든 ) 수이기 때문에 원을 쪼개서 계산할 때 유용하다.
호도법(Radian)
1도씩 단위로 삼아 원에 관련된 수학을 전개했을 때 불편한 점이 많다. 따라서 별도의 단위를 정하고 이를 기준으로 원에 대한 수학을 전개할 때 사용한다.

반지름이 1인 반원을 생각해보자

이 반원을 원점으로 이동시킨 후 펼치면
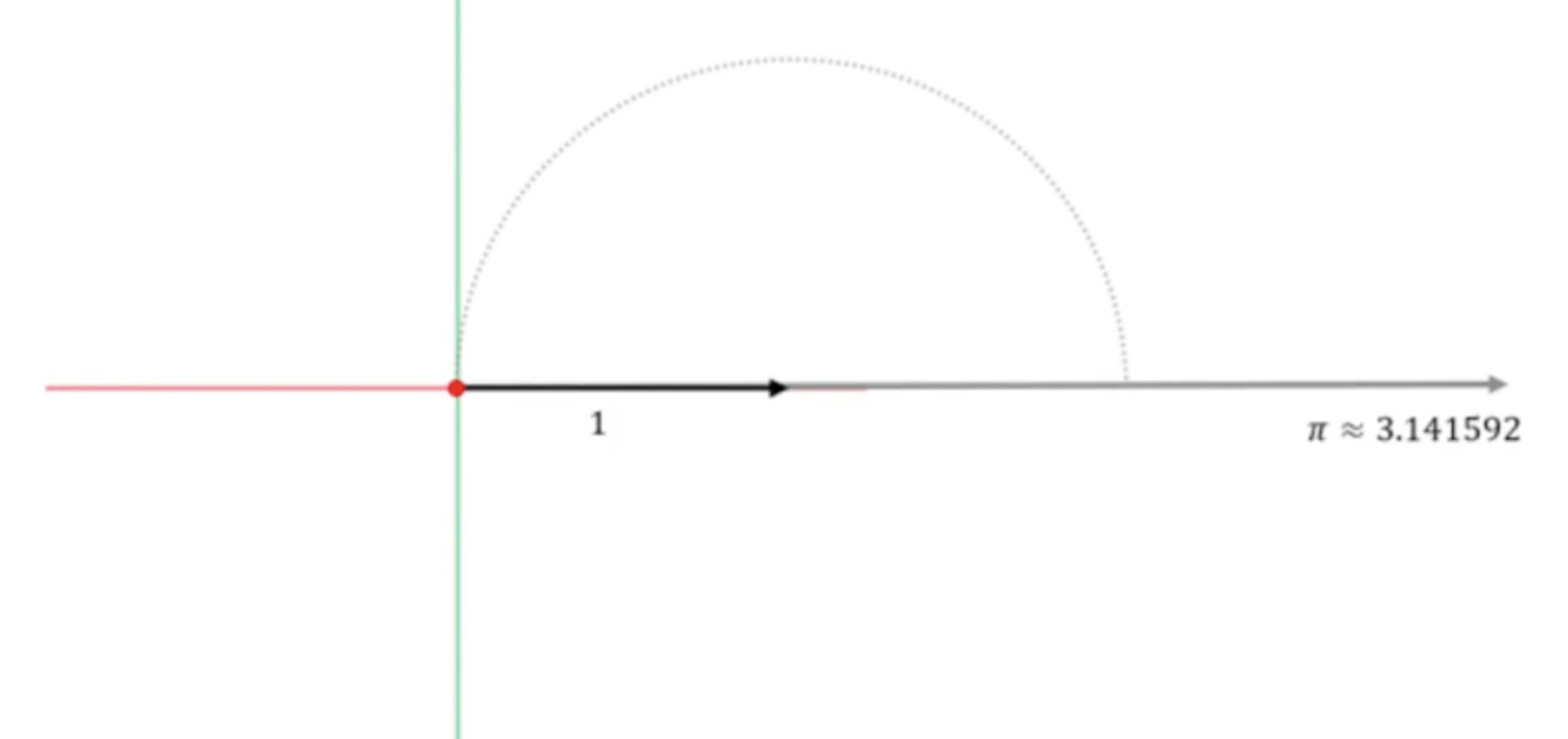
다음과 같이 원호의 길이를 잴 수 있게 된다.
이 길이가 3.141592... 인 ℼ 이다.
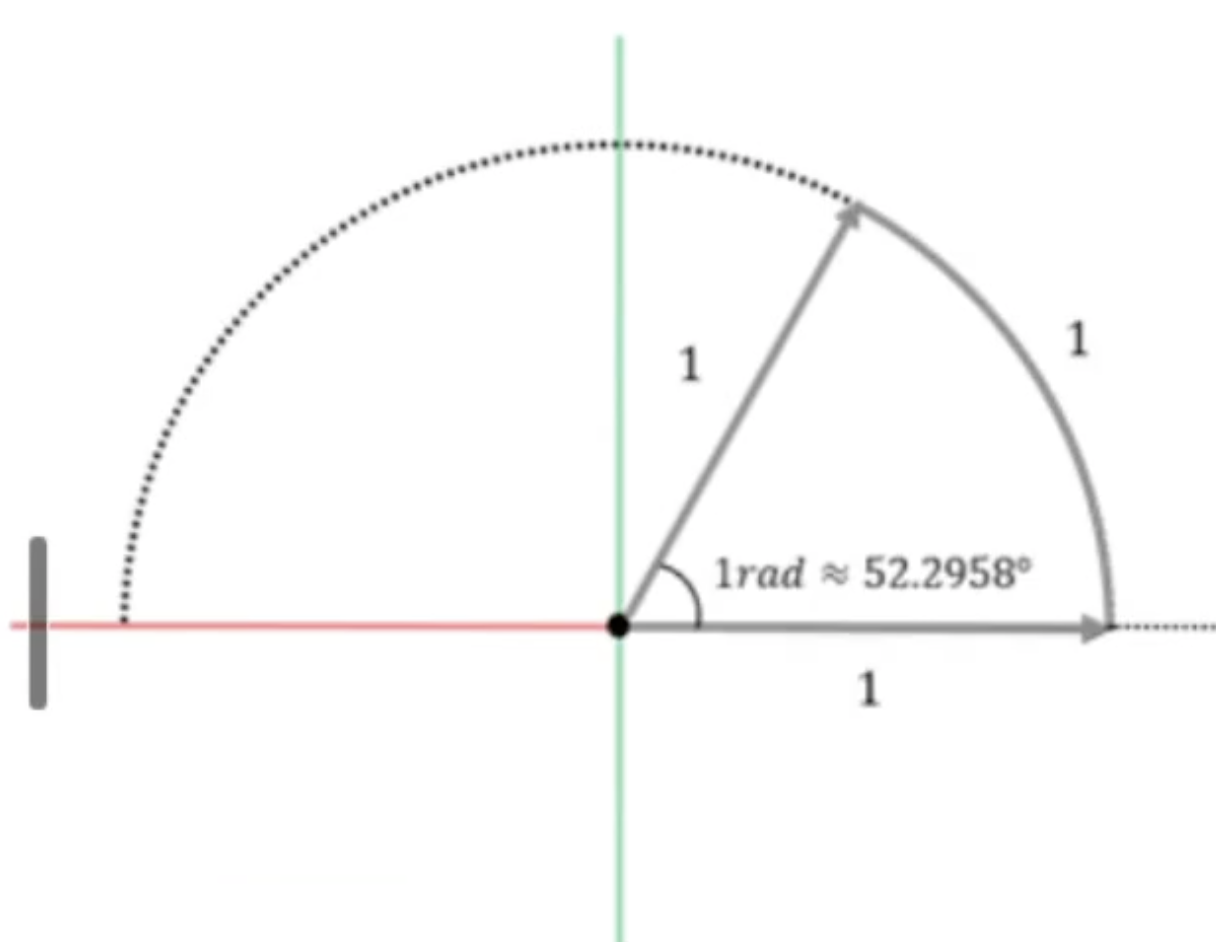
이 때 크기가 1만큼이 펼쳐진 반원에서 어느정도인지를 확인해보면
약 52.2958도이고 이 것이 1 radian 이다.

이로부터 유도되는 호도법과 각도법의 관계는 다음과 같다.
역함수
역함수가 존재하기 위해서는 해당 함수는 전단사함수여야 한다.
하지만 sin, cos, tan 는 전단사 함수가 아니다. (단사가 아니다. 여러개의 정의역이 하나의 치역에 대응될 수 있다.)
따라서 sin, cos, tan 함수를 단사함수로 만들기 위해 의도적으로 정의역의 값을 제한시킨다.
그렇다면 전단사함수가 되어 역함수가 존재할 수 있다
sin : $$[-\frac{\pi}{2}, \frac{\pi}{2}]$$
cos : $$[0, \pi]$$
tan : $$(-\frac{\pi}{2}, \frac{\pi}{2})$$
위의 범위에서 정의한 역함수를 arcsin, arccos, arctan 함수라고 부른다.



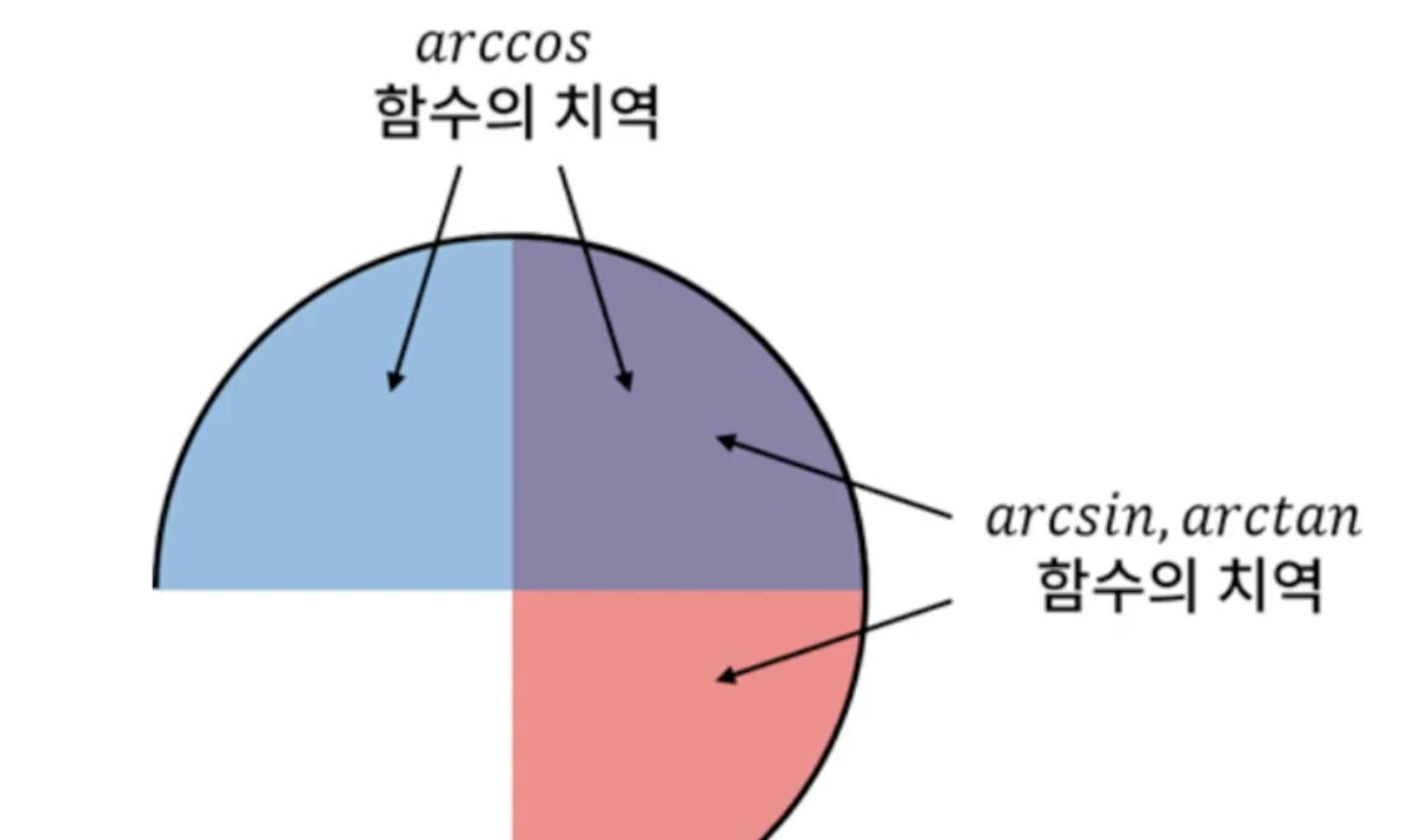
역함수를 통해 대응되는 각을 알아낼 순 있지만, 3사분면의 값은 알아낼 수 없다. (치역의 범위를 보자)
이를 위해 아크탄젠트를 사용할때 부호를 확인하여 처리한다.

아크탄젠트 함수에 대응되는 치역은 동일하지만, x 와 y의 부호를 가지고 3사분면의 각을 알아낼 수 있다.
(여기서 x, y는 cos, sin 으로 알수있다는 사실을 기억하자)
이것이 우리가 사용하는 atan2(y, x) 함수이다.
어떤 벡터의 각을 알고싶다면 탄젠트의 역함수 atan2를 사용한다.
극좌표계

데카르트 좌표계에서 극 좌표계로 변환

극좌표계에서 데카르트 좌표계로 변환
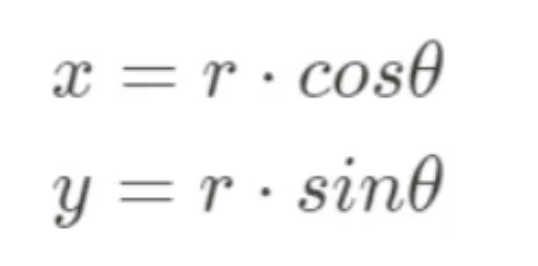
'Graphics > 이론' 카테고리의 다른 글
| 픽셀화 ( Rasterization ) (1) | 2022.12.28 |
|---|---|
| 아핀 결합 ( Affine Combination ) (1) | 2022.12.21 |
| 원근 투영 변환 - 깊이값( Perspective projection transformation - Depth ) (1) | 2022.11.17 |
| 원근 투영 변환 ( Perspective projection transformation ) (4) | 2022.11.14 |
| 뷰 변환 ( View Transformation, Camera Transformation ) (0) | 2022.11.08 |
