이 글을 읽는 사람이 기초 개념을 알고있다고 가정합니다. ( 선형성, 행렬 등 )
월드 변환이란?
월드 변환은 모델의 로컬 원점을 기준으로 Vertex가 정의된 모델 공간에서 모든 개체에 공통된 원점을 기준으로 정의되는 World Space로 좌표를 변경하는 것이다.
월드 변환에는 좌표 이동, 회전 및 크기 조정이 포함될 수 있다.
월드 변환을 알기 전에 '좌표 이동', '회전', '크기' 조정에 대해 알아야 한다.
이동 변환
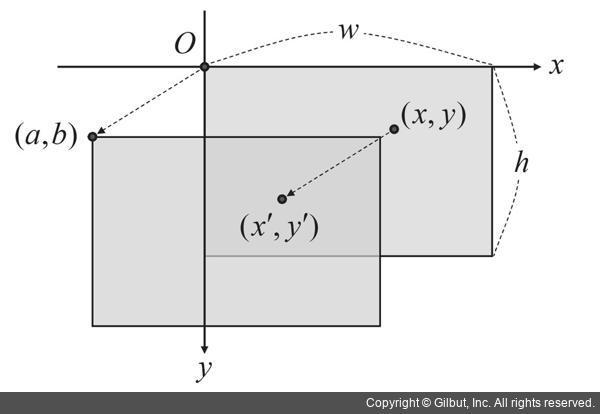
말 그대로 어떠한 Vertex를 특정 크기만큼 이동시키는 변환을 의미한다.
이동 변환을 수식으로 표현하면 다음과 같다.
$$\begin{cases}x' = x + a\\y' = y + b\\z' = z + c \end{cases}$$
이동 행렬은 다음과 같다.
$$ \begin{bmatrix}x & y\\ \end{bmatrix} +
\begin{bmatrix} a & b\\ \end{bmatrix} =
\begin{bmatrix}x + a \\y + b \end{bmatrix} $$
(회전, 크기 변환에 대해 설명한 후 자세히 다룰거니 일단 이것만 알아두자)
회전 변환
회전 변환은 특정 '점' 을 좌표내에서 각도만큼 회전시켜주는 변환이다.
일단 이에 대해 유도를 해보자.
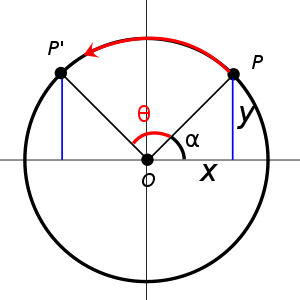
P(x, y) 가 P' (x', y')로 $$\Theta $$ 만큼 회전했다고 생각해보자.
일단 P의 x, y를 계산해보자
$$\frac{x}{r} = cos\alpha$$ 이고
$$\frac{y}{r} = sin\alpha$$ 이므로
$$x = rcos\alpha$$
$$y = rsin\alpha$$ 이다.
그럼 P'(x', y')는 $$\alpha$$에 $$\theta$$ 를 더 한 것이므로
$$x' = rcos(\alpha + \theta)$$
$$y' = rsin(\alpha + \theta)$$ 이다.
이걸 삼각함수 합차공식으로 정리하면
$$x' = rcos\alpha\cos\theta\ - rsin\alpha\sin\theta$$
$$y' = rsin\alpha\cos\theta\ + rcos\alpha\sin\theta$$ 이다.
$$x = rcos\alpha$$
$$y = rsin\alpha$$ 이므로 치환하면
$$x' = xcos\theta\ - ysin\theta$$
$$y' = ycos\theta\ + xsin\theta$$ 이다.
이를 행렬로 정리하면
$$\begin{bmatrix}x & y \end{bmatrix}
\begin{bmatrix}cos\theta & sin\theta \\-sin\theta & cos\theta \end{bmatrix}$$
이고 이것이 곧 회전 변환 행렬이다..
크기 변환
크기 변환은 물체의 크기를 변경하는 변환이다.
크기 변환은 각 표준기저벡터를 동일한 방향으로 지정한 크기만큼 늘리는 변환을 의미한다.
이를 위해 (1, 0) 좌표를 갖는 e1 과 (0, 1) 좌표를 갖는 e2 표준기저벡터를 생각해보자.
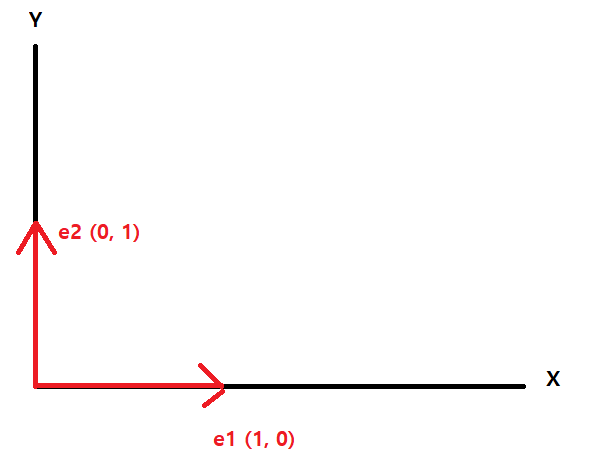
표준기저벡터 e1을 a배 늘리거나 줄인 벡터 = $$a \cdot(1, 0) = (a, 0)$$
표준기저벡터 e2를 a배 늘리거나 줄인 벡터 = $$b \cdot(0, 1) = (0, b)$$
e1을 a배 만큼 늘리고, e2를 b배만큼 줄인 선형 변환으로 인한 벡터의 좌표는 다음과 같다.
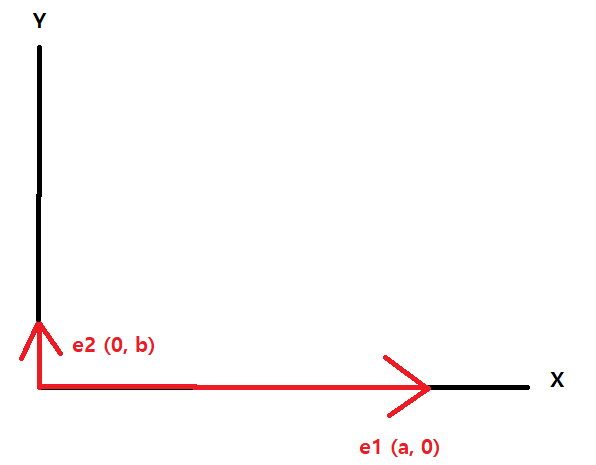
그렇다면 변환된 두 표준기저벡터 (a, 0)과 (0, b)를 행벡터로 설정해 생성한 크기 변환행렬은 다음과 같다.
$$S = \begin{bmatrix}a & 0 \\0 & d \end{bmatrix}$$
전단 행렬
위의 월드 변환과는 상관 없지만, 앞으로의 설명을 위해 작성한다.
표준 기저 벡터 e1, e2가 있을 때 e2를 x축 방향으로 미는 변환을 생각해보자
e1은 고정되어 있기 때문에, 변환된 결과는
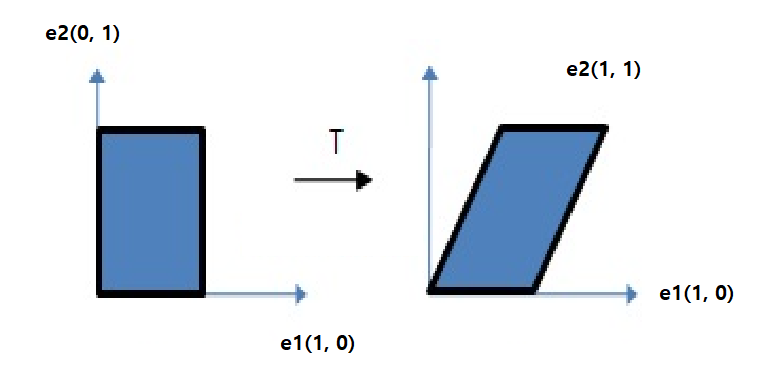
다음과 같이 될 것이다.
표준기저벡터 e2를 x축 방향으로 1만큼 밀어내는 전단 변환행렬은 다음과 같다
$$S = \begin{bmatrix}x & y \end{bmatrix}\begin{bmatrix}1 & 1 \\0 & 1 \end{bmatrix}$$
그러므로 x축 방향으로 a만큼 미는 전단 변환행렬은 다음과 같다.
$$S =\begin{bmatrix}1 & a \\0 & 1 \end{bmatrix}$$
아핀 변환 (Affine Transform)
이렇게 크기 + 회전 + 이동 을 하나의 '점' 또는 '도형'에 변환시킨 것을 아핀변환이라고 한다.
$$v' = v \cdot\ S\cdot\ R + T$$
아핀 변환은 기본적으로 '비선형' 변환이다. 그러므로 선형성을 만족하지 않는다. ( 이동 때문 )
몇천개의 Vertex에 해당 변환을 순서대로 작업하는것은 성능에 문제가 될 수 있다.
이를 위해서 이동 변환이 선형성을 만족하는 선형 변환으로 변환한다.
곱셈으로 변화시킬 필요성이 있는데 (선형성을 만족하기 위하여) 아무리 생각해도
$$ \begin{bmatrix}x & y \end{bmatrix}
\begin{bmatrix}a & b \\c & d \end{bmatrix}
= \begin{bmatrix}x + e & y + f \end{bmatrix} $$
같은 행렬은 존재하지 않는다.
대신 위에서 설명했던 전단 변환을 사용하여 처리해보자
전단 변환을 사용하면 하나의 표준 기저 벡터를 미는 것 (이동) 이 가능했다.
즉 (e1, e2)에서 e2의 x만 변경하게 됐는데, 이를 1이라는 값을 추가해 3차원으로 변경해본다.
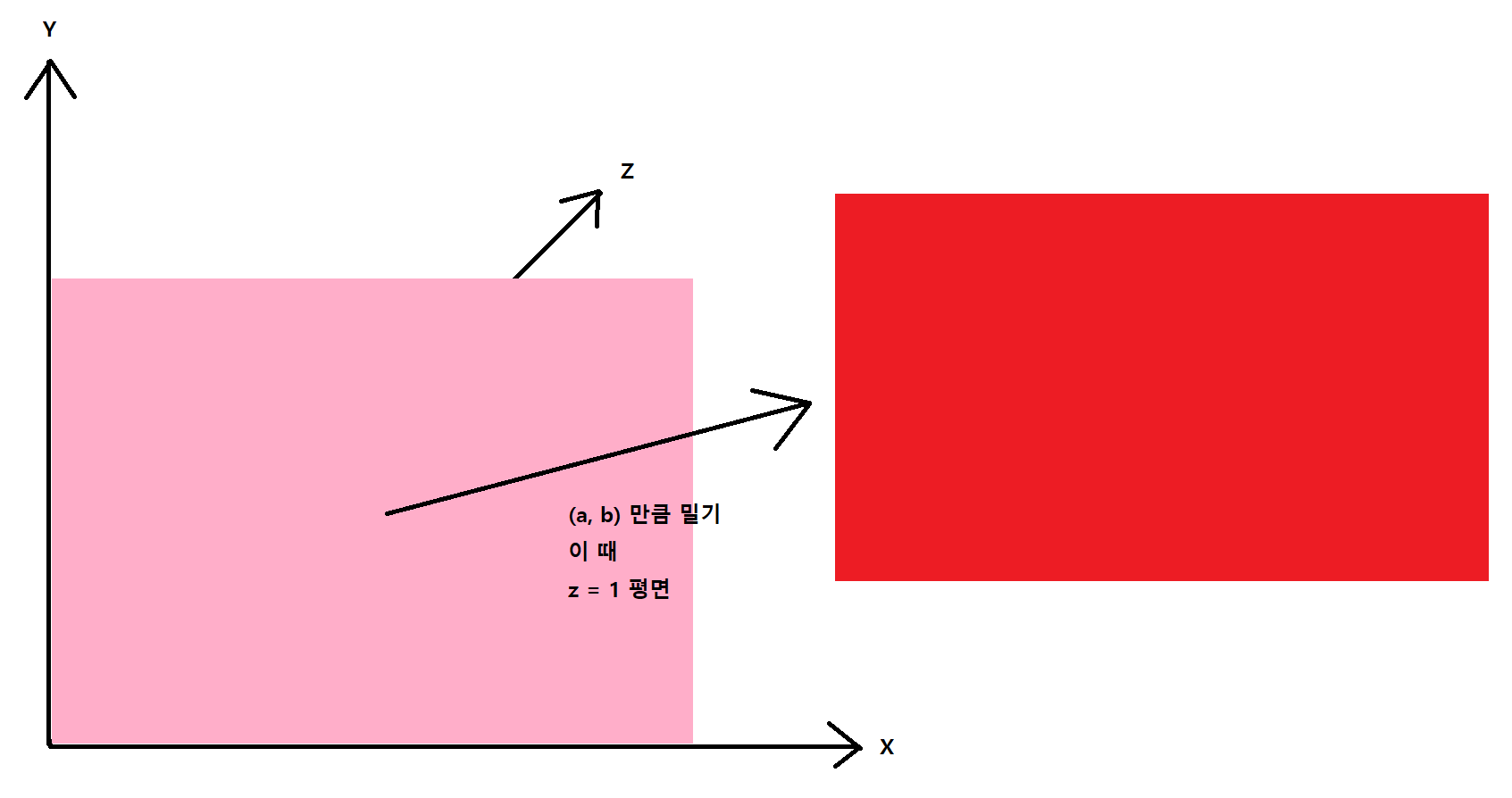
이렇게 3차원인 공간에서 x축과 y축을 (a, b) 만큼 밀었을때 z는 1인 평면상에서 이동한 결과를 가지게 된다.
$$\begin{bmatrix}x & y & 1 \end
{bmatrix}\begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\ a & b & 1 \end{bmatrix}
= \begin{bmatrix}x + a & y + b & 1 \end{bmatrix}$$
이렇게 한 차원 위에서 변환 작업을 하면 이동, 회전, 크기 변환을 선형적으로 처리할 수 있는데 이러한 변환을 (선형적인) 아핀 변환 이라고 한다.
이동, 회전, 크기 변환이 모두 선형적이기 때문에 이를 하나의 행렬로 처리할 수 있다.
동차좌표
이동은 행렬곱에서 선형적이지 않았다. (위에서 말한 덧셈요소 때문이다.)
이를 위해서 우리는 한 차원을 올리고 밀기 연산을 통해서 선형적으로 처리할 수 있었는데,
이렇게 이동까지 곱셈으로 만들기 위해 한 차원을 올린 좌표계를 '동차좌표계' 라고 한다.
(동차좌표의 자세한 설명은 하지 않는다, x, y, z, 1 / wx, wy, wz, w 같은걸 설명해봤자 초보자에겐 이해가 안된다. 나중에 원근투영에서 다시 다룬다.)
이제 3차원에서의 변환을 생각해보자
회전과 크기는 3 x 3의 행렬로 처리할 수 있으나, 이동은 한 차원을 올린 동차좌표계에서만 처리가 가능하다
(즉 이동 행렬은 이 상태에선 4 x 4 의 동차좌표이다)
이를 위해 회전과 크기도 동차좌표계로 변경한 후 선형변환한다.
$$ \begin{bmatrix}Sx & 0 & 0 & 0 \\0 & Sy & 0 & 0 \\ 0 & 0 & Sz & 0 \\ 0 & 0& 0& 1\end{bmatrix}
\begin{bmatrix}Xx & Xy & Xz & 0 \\Yx & Yy & Yz & 0 \\ Zx & Zy & Zz & 0 \\ 0 & 0& 0& 1\end{bmatrix}
\begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ x & y & z& 1\end{bmatrix} = SRT $$
이것이 월드변환의 최종 행렬 식이다.
( 회전은 오일러 변환을 사용했다. 오일러 변환을 사용하지 않을거면 x, y, z 순서를 맞춘 후 앞에서 설명했던 회전 행렬의 Rx, Ry, Rz 회전을 적용시키면 된다. 오일러 변환에 대해서는 하나의 글로 따로 다룰것이기 때문에 이 글에서는 다루지 않는다.)
'Graphics > 이론' 카테고리의 다른 글
| 아핀 결합 ( Affine Combination ) (1) | 2022.12.21 |
|---|---|
| 원근 투영 변환 - 깊이값( Perspective projection transformation - Depth ) (1) | 2022.11.17 |
| 원근 투영 변환 ( Perspective projection transformation ) (4) | 2022.11.14 |
| 뷰 변환 ( View Transformation, Camera Transformation ) (0) | 2022.11.08 |
| 오일러 변환 (Euler Transformation) (0) | 2022.10.31 |
